
|
|
日本早稻田大学图书馆所藏水浒画册,标题就有“百八人像”的提法 |
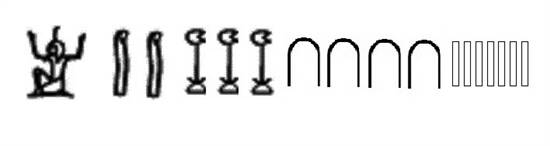
|
|
用古埃及数字表示1023407 |

|
|
古希腊数字与阿拉伯数字对照表 |
|
|
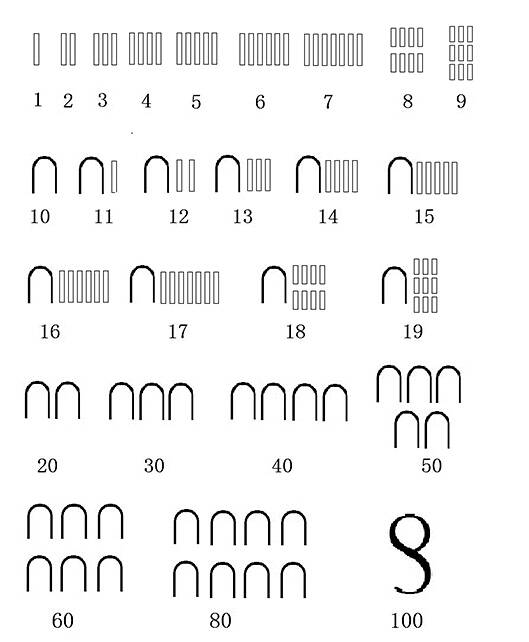
古埃及数字:1到100 |

|
|
古埃及数字:1到100万 |
□撰文/供图 李开周 清朝以前数字里都没有零 零作为数字的历史很晚很晚才出现,宋朝的数字里没有零,元朝和明朝的数字里也没有零。小说家施耐庵生活在元末明初,他写《水浒传》,写到梁山泊好汉人数,通常是“一百八人”或者“一百八员”。 例如该书第七十回,宋江先打东平府,再打东昌府,回到山寨,对众弟兄说:“共聚得一百八员头领,心中甚喜。” 再比如第七十一回,宋江率领大家在忠义堂对天盟誓,誓词是这么说的:“宋江鄙猥小吏,无学无能,荷天地之盖载,感日月之照临,聚弟兄于梁山,结英雄于水泊,共一百八人……” 还有第八十二回,太尉宿元景回奏:“宋江等军马,俱屯在新曹门外,听候圣旨。”宋徽宗说:“寡人久闻梁山泊宋江等一百八人,上应天星……” 近现代说书人演绎《水浒传》,张口闭口“一百零八条好汉”,这其实是清朝以后才有的说法,清朝以前只能是“一百八条好汉”,没那个“零”。20世纪初,考古人员在甘肃敦煌千佛洞发现唐朝数学文献《立成算经》,里面记录钱币数字108文,也是写成“一百八文”,而不是“一百零八文”。 我们必须说明,中国古籍里并不是没有零,只不过,那些零的含义与数字无关。它们有时是“凋零”的零,有时是“零散”的零,有时是“挂零”的零。它们可以有“滴落”的意思,可以有“细碎”的意思,可以有“附加”的意思,却没有“一减一等于零,零加零还是零”的意思。 偌大一个中国,堂堂几千年文明,怎么就认识不到零也是一个数字,并且还是一个非常关键的数字呢? 其实,不只是古代中国没有数字零,古希腊、古罗马和古埃及也没有数字零。在任何一个古典文明时代,一切数学概念和数学技能都是因为实际需要,才不得不发明出来的,而零在很长时期内都没有被发明的必要。什么是零?不就是空无所有吗?每个数字都被用来计算那些实实在在的东西,空无所有的东西凭什么需要数字呢?空无所有的数字怎么能够进行计算呢? 数字用来描述实有,虚空之物不需要数字,这是非常朴素的想法,自自然然,水到渠成,认识不到零很正常,认识到应该有零,那才叫稀奇古怪、异想天开。 没有零一样记数和计算 现代人写数字和做运算,绝对离不开零。11+19=30,一个零出来了。111-11=100,两个零出来了。古中国、古希腊、古罗马、古埃及都没有零,先民们如何计算?如何进位?如何用数字表示几十、几百、几千、几万呢? 早期文明的数字符号告诉我们,即使没有零,一样可以表示很大的数字,只不过表示方法要复杂一些。 以古埃及为例,1的符号是一竖,像一根棍子;2的符号是两竖,像两根棍子;以此类推,3是三根棍子,4是四根棍子,5是五根棍子……到了10,符号变成一道拱形(据说这个符号是一只踝骨),好像字母n,又像集合运算符号里计算交集的∩。然后呢?11是一道拱加一竖,12是一道拱加两竖,13是一道拱加三竖……到了20,用两道拱来表示;30是三道拱,40是四道拱,50是五道拱……100呢?被写成一个曲里拐弯的符号,仿佛缺了左下角的8,又仿佛头朝上的小蝌蚪。 比100还要大的数字,古埃及人也能写出来,例如1000像一支火炬(也有人说这是一朵莲花),1万像一根手指,10万是一只神鸟,100万是一个单膝跪地、双手投降、仿佛被这个巨大数字吓怕了的人。 古埃及人如果要写1023047这个数字,会画一个受惊吓的人,表示100万;再画两根手指,表示2万;再画三支火炬,表示3000;再画四个拱形,表示40;最后画七根棍子,表示7。整个数字写出来,会是这个样子: 古埃及数字是象形符号,古希腊和古罗马则用字母表示数字。在古希腊,1被写成A,2被写成B,3被写成Γ,4被写成△,5是E,6是F,7是Z,8是H,9是θ,10是I,11是IA,12是IB,13是IΓ,14是I△……20被写成K,21写成KA,22写成KB,23写成KΓ,100写成P。如果想写108,那就是PH,中间不需要一个表示零的符号。 相对而言,我们对古罗马数字更加熟悉,生活当中也能见到它们。在一些钟表上,从1点钟到12点钟,分别用Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ、Ⅷ、Ⅶ、Ⅷ、Ⅸ、Ⅹ、Ⅺ、Ⅻ来表示。而那些稍大一些的数,会被写成不同的字母或者字母组合,例如50是L,100是C,500是D。古罗马人想记录一个数字,先看这个数能不能对应一个现成的字母,如果不能,那么分解这个数,把它分解成几个字母。 比如说,要写100,用一个字母C就行。要写200,就得写成CC。写230呢?因为230等于100+100+30,而30又等于10+10+10,100的对应字母是C,10的对应字母是X,所以230被记作CCXXX。再比如732,可以分解成500+100+100+10+10+10+2,其中500用D表示,100用C表示,10用X,2用Ⅱ,732会被写成DCCXXXⅡ。像这样的数字系统,记录繁琐,识别易错,计算之时更加令人头疼(不能像阿拉伯数字那样将不同数字的相同数位对应起来,以便加减乘除),但自始至终都不需要有零参与。

